EM 알고리즘은 두단계를 거치는데
첫번째 단계는
E단계( Expectation step )
두번째 단계는
M단계( Maximization step )이다.
running 과정에서는 이 두 단계가 계속 반복된다.
간단한 예를 살펴보면
1. 초기값 설정
2. 반복 과정
2.1 E-STEP : 주어진 현재 파라미터 추정치로 unknown 변수가 특정 class에 속하는지에 대한 기대값을 추정한다.
2.2 M-STEP : unknown 변수의 기대 추정치를 가지고 데이터의 최대 확률값(MLE)을 재 추정한다.
EXAMPLE >
[STEP1] 4,10 , ? , ?Initial mean value : 0
[STEP2] 4, 10, 0 , 0
New Mean : 3.5{ ( 4 + 10 + 0 + 0 ) /4 }
[STEP3] 4, 10, 3.5, 3.5
New Mean : 5.5
[STEP4] 4, 10, 5.25, 5.25
New Mean : 6.125
[STEP5] 4, 10, 6.125, 6.125
New Mean : 6.5625
[STEP6] 4, 10, 6.5626, 6.5625
New Mean : 6.7825
[STEP7] 4, 10, 6.7825, 6.7825
이 과정을 반복하다 보면 Mean이 7에 가까워지는것을 볼 수 있다.
파라미터를 추정하는 방법론이기 때문에 수렴 속도가 빨라지거나 하지는 않는다
LINK : http://en.wikipedia.org/wiki/Expectation-maximization_algorithm
LINK : Foundations of Statistical Natural Language Processing
LINK : http://nlp.korea.ac.kr/new/seminar/2000spring/fsnlp/Chap14_Clustering.ppt
-----------------------------------------------------------------------------------------------------
Expectation Maximization 말그대로 Expectation(기대값)이 최대가 대는 모델( 파라미터 )을 찾는 방법을 의미한다.
다른 예제
두개의 동전이 있다.
첫번째 동전을 A
두번째 동전을 B 로하자
두개의 동전은 다른 동전과는 달리 앞면과 뒷면이 나올 확률이 균일하지 않다.
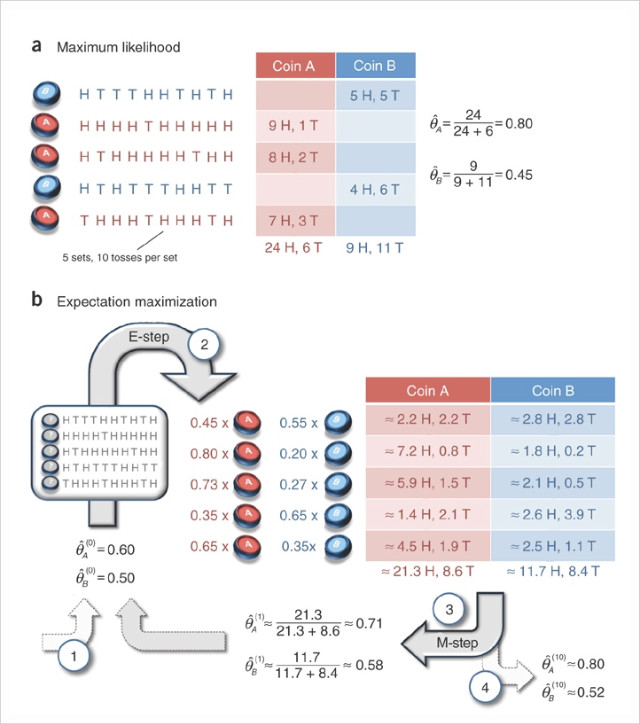
하나의 동전을 10번씩 던지는 실험을 총 5회에 걸쳐 실험을 했더니
test1: H T T T H H T H T H
test2 : H H H H T H H H H H
test3: H T H H H H H T H H
test4 : H T H T T T H H T T
test5 : T H H H T H H H T H
위과 같은 실험 결과가 나왔을때
동전 A가 H가 나올 확률과
동전 B가 H가 나올 확률을 구하라
초기값으로
첫번째 동전이 앞면이 나올 확률을 0.6
두번째 동전이 앞면이 나올 확률을 0.5라고 하자( 임의 )
test1을 기준으로 보면
H 가 5번 T 이 5번이다.
첫번째 동전을 던져서 나올 확률 값이라고 가정을 하고
test1의 확률을 계산하면( 이항분포 )
0.6^5 * (1 - 0.6)^5 = 0.07776 * 0.01024 = 0.0007962624 - (1)
두번째 동전을 던져서 나올 확률 값이라고 가정을 하고
test1의 확률을 계산하면
0.5^5 * ( 1- 0.5 )^5 = 0.03125 * 0.03125 = 0.0009765625 - (2)
0.0007962624 + 0.0009765625 = 0.0017728249
(3) = (1) + (2)
(1)/(3) = 0.0007962624 / 0.0017728249 = 0.4491489261009364207373215482251 = 약 0.45
(2)/(3) = 0.0009765625 / 0.0017728249 = 0.5508510738990635792626784517749 = 약 0.55
즉 test1은 첫번째 동전일 확률이 0.45이고 두번째 동전일 확률은 0.55가 된다.
이와 같은 방법으로 5번의 테스트에 대해서 확률 값을 구하면
첫번째 동전이 H일 확률은 0.80로
두번째 동전이 H일 확률은 0.52로 수렴한다.
LINK : http://www.nature.com/nbt/journal/v26/n8/full/nbt1406.html
'언어처리' 카테고리의 다른 글
| auto tagging (0) | 2008.10.29 |
|---|---|
| Yi Syllables - 0xa0c2 (0) | 2008.10.07 |
| 제20회 한글 및 한국어 정보처리 학술대회 (0) | 2008.09.01 |
| 영작 하는 법 (0) | 2008.07.24 |
| 아랍어 테스트 (0) | 2008.07.24 |