초간단 예제
F(x,y) = x + y이고
이것의 제한 조건이 x^2 + y^2 = 1일때
이 두개를 만족하는 해 중에 최대값은  이고, 최소값은
이고, 최소값은  이다.
이다.
g(x,y) - c = x^2 + y^2 - 1
Λ(x,y,λ) = f(x,y) + λ(g(x,y) − c) = x + y + λ(x2 + y2 − 1)
을 편미분 한다.
첫번째로 x로 편미분 하면
두번째는 y로 편미분 하고
세번재는 lambda로 편미분하면( lambda =  )
)
아래와 같이 3개의 다항식을 얻을수 있다.
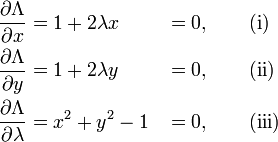
보통 (iii) lamba로 편미분한 다항식은 처음 조건으로 제시된 제한 조건과 일치한다.
처음 두개의 다항식{ (i),(ii) }를 결합하면
1 + 2Lx = 1 + 2Ly (L : lambda )
2Lx = 2Ly
x = y가 된다.
따라서 세번째식 x^2 + y^2 = 1을
x^2 + x^2 = 1 => 2x^2 = 1로 변환할수 있고
x^2 = 1/2 가 되고 결국 x =  또는
또는  라는 해를 얻을수 있다.
라는 해를 얻을수 있다.
이 해를 함수에 적용해보면
 가 되고
가 되고
결국 제한조건을 만족하는 함수 f의 최대값은  가 되고 최소값은
가 되고 최소값은 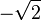 가 된다.
가 된다.
간단 예제
f(x,y) = x^2y이고
제한조건이 x^2 + y^2 = 3일때
g(x,y) - c = x^2 + y^2 - 3이다.
 에서
에서
첫번째로 x로 편미분 하면
두번째는 y로 편미분 하고
세번재는 lambda로 편미분하면
아래와 같이 3개의 다항식을 얻을수 있다.
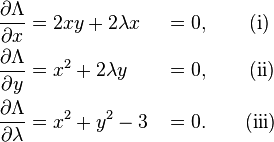
첫번째 다항식에서 x = 0이거나 lambda가 -y이면 첫번째 다항식을 만족한다.
만약 x = 0일 경우를 보면  가 되고 lambda = 0이된다.
가 되고 lambda = 0이된다.
lambda = -y라면
두번째 다항식에 적용하면 다음과 같이 된다.
x^2 - 2y^2 = 0 => x^2 = 2y^2
다시 세번째 다항식에 적용하면
2y^2 + y^2 -3 = 0 => 3y^2 = 3 => y^2 = 1
 이 된다.
이 된다.
따라서 해는
 가 되고
가 되고
우리가 찾고자 하는 값은

global maximum : 
local maximum : 
local minimum :  을 얻을수 있다.
을 얻을수 있다.
comment : 함수가 주어지고 이 함수에 대한 특정 제한 조건이 존재할때, 이 제한 조건을 만족하는 최대값과 최소값을 라그랑제 승수로 구할수 있다.
'알고리즘' 카테고리의 다른 글
| mapreduce and (in) search (0) | 2011.05.17 |
|---|---|
| Animation of Lempel-Ziv Encoding Algorithm (0) | 2010.09.28 |
| 최대 엔트로피 모델( Maximum Entropy Model ) (0) | 2009.09.04 |
| LINGO Algorithm (0) | 2009.08.25 |
| Probabilistic Semantic Latent Analysis (0) | 2009.06.25 |