희소행렬 (sparse matrix) - yale format
희소 행렬을 표현하는 여러가지 방법이 있다.
그 중 Yale format에 대해 알아보자
예일포맷(Yale format)
Yale format
The Yale Sparse Matrix Format stores an initial sparse m×n matrix, M, in row form using three one-dimensional arrays. Let NNZ denote the number of nonzero entries of M. The first array is A, which is of length NNZ, and holds all nonzero entries of M in left-to-right top-to-bottom (row-major) order. The second array is IA, which is of length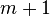 
(i.e., one entry per row, plus one). IA(i) contains the index in A of the first nonzero element of row i. Row i of the original matrix extends from A(IA(i)) to A(IA(i+1)-1), i.e. from the start of one row to the last index before the start of the next. The third array, JA, contains the column index (zero-based) of each element of A, so it also is of lengthNNZ. For example, the matrix
-
-
[ 1 2 0 0 ][ 0 3 9 0 ][ 0 1 4 0 ]
-
is a three-by-four matrix with six nonzero elements, so
A = [ 1 2 3 9 1 4 ](array of non-zero element values)IA = [ 0 2 4 ](array of index of first nonzero element of rowi)JA = [ 0 1 1 2 1 2 ](array of column index of eachAelement)
A : 0이 아닌 값 배열
IA : 0이 아닌 최초의 값이 나타나는 행의 위치
첫번째 행에 0이 아닌 값이 2개, 두번째 행에 0이 아닌 값이 2개, 세번째 행에 0이 아닌 값이 2개, 따라서 0 2 4 6
JA : 행 단위로 0이 아닌 값의 컬럼 INDEX
0 1 2 3
0 [ 1 2 0 0 ]1 [ 0 3 9 0 ]2 [ 0 1 4 0 ]
JA가 어떻게 만들어지는 간단히 살펴보면
첫번째 행을 보면
0 1 2 3 <- 컬럼 index
0 [ 1 2 0 0 ]
1 컬럼의 위치는 0이고
2 컬럼의 위치는 1이다.
두번째 행을 보면
0 1 2 3 <- 컬럼 index
1 [ 0 3 9 0 ]
3 컬럼의 위치는 1
9 컬럼의 위치는 2
세번째 행을 보면
0 1 2 3 <- 컬럼 index
2 [ 0 1 4 0 ]
1 컬럼의 위치는 1
4 컬럼의 위치는 2
나열하면 0 1 1 2 1 2 가 된다.